Four fundamental forces are known in physics: the weak and strong interactions, and the electromagnetic and gravitational forces. Gravity is the weakest of these four. For this reason, and because experiments cannot be protected from the earth’s gravity, it is difficult in the laboratory to make measurements of the gravitational field of a test object – even for objects with a mass of more than one kilogram. But sign up Nature, Westphal et al.1 reports the detection of the gravitational coupling between two masses of only about 90 milligrams.
The weak, strong and electromagnetic interactions are united in the standard physics model, but the gravitational force cannot be integrated in the model. The best model currently available to describe gravity is the general theory of relativity. This theory has so far failed any test, but something is strange about it, because it can not be explained by quantum mechanics.
For most scientific purposes, however, we do not have to use the general theory of relativity to explain gravity – Isaac Newton’s law of universal gravitation2 works perfectly. Newton’s law, published in 1687, states that the force of attraction between two bodies is proportional to their masses and inversely proportional to the square of the distance between them. This appears to be not only correct for describing most astronomical observations, but also in laboratory experiments. For example, the trajectory of an object falling free (like an apple falling from a tree) can be measured with a precision of less than ten parts in a billion3, and the results agree well with what would be expected from Newton’s law.
During the twentieth century, however, doubts arose about the general correctness of this law: a deviating velocity distribution of stars in galaxies was observed.4 in the early thirties, and could not be explained by Newton’s law5. Even the general theory of relativity cannot account for this phenomenon. One explanation is to postulate the existence of dark matter6 – an invisible but gravity-generating component of the Universe. However, no one really knows what this dark matter consists of.
A further statement, which is controversial but easier to integrate into models than dark matter, is that Newton’s law of gravity needs to be corrected. One theory that attempts to make such a correction was proposed in the 1980s and is called the modified Newtonian dynamics.7. The basis of this theory is that gravitational field strength (the acceleration due to gravity) does not follow Newton’s inverse square law over long distances.
A further mystery is that the gravitational force is about 36 orders of magnitude weaker than the electromagnetic force. This is called the hierarchy problem8.
A framework known as string theory, developed in part to provide a quantum theoretical description of gravity, addresses this problem by suggesting that there are more spatial dimensions than the three we can observe. Gravity – unlike the other three fundamental forces – is believed to permeate these extra dimensions. If this is true, it may explain why gravity is so much weaker than electromagnetic force9. Another consequence would be that the gravitational force over a certain spatial extent cannot be described by Newton’s inverse-square law.
A further peculiar thing about gravity is that independent measurements of Newton’s gravitational constant (G, a fundamental constant used in calculations of gravitational effects, varied widely10. Experimental determinations of other fundamental constants, such as the Boltzmann constant11 or the speed of light12, coincided as the number and accuracy of the measurements increased. It has not happened yet G.
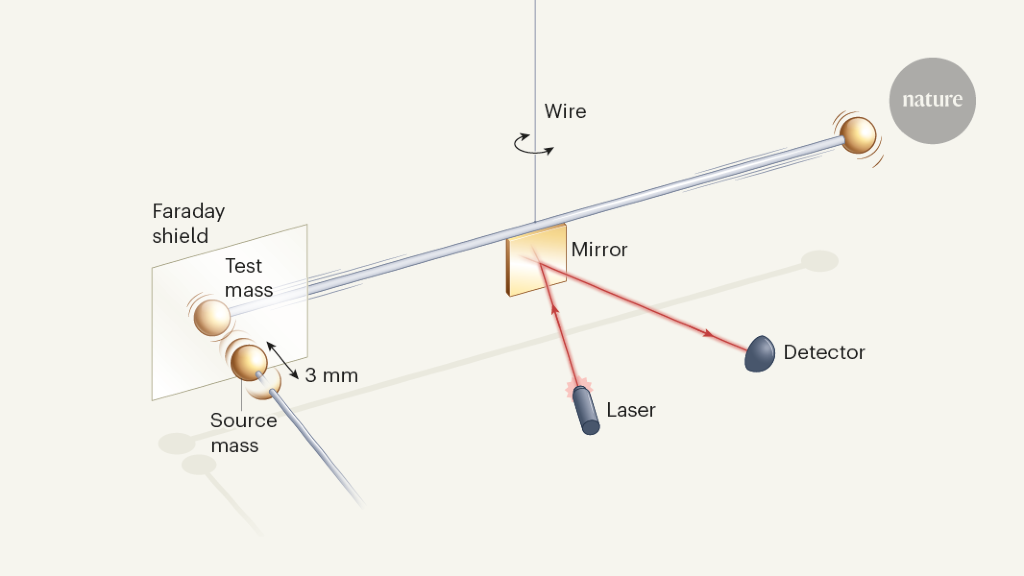
Westphal and colleagues’ experiments can bring us one step closer to understanding the mysteries of gravity. They investigated the gravitational force using a miniature version of a torsional balance – a device first used by Henry Cavendish in 1798 to measure the density of the earth.13 (an experiment equivalent to measuring G), and what is still the gold standard device to determine G14.
A torsion balance consists of a horizontal bar that hangs in the middle of a vertically hanging wire and with test masses attached to the ends. Earth’s attraction acts in the vertical direction, along which the wire has a great rigidity. But in the horizontal direction, the wire can be easily twisted and it has a small spring constant – very weak forces applied at right angles to the rod cause large rotations of the rod. The balance thus generates an almost gravitational-free environment (more accurately described as a microgravity) in the horizontal plane. It is ideal for detecting small forces, such as the force of gravity exerted by a nearby object (the source mass) on the rod.
In typical terms of G, the source masses were heavy (a few kilograms), to compensate for the weakness of gravity. In contrast, Westphal and associates used gold spheres only 92 milligrams in mass (Fig. 1), about the mass of 4 houseflies. This is the lowest source mass ever used in such an experiment.
Figure 1 | How to detect a weak gravitational field. Westphal et al.1 hangs a horizontal bar on a wire, with two masses of about 90 milligrams on each side. Then they brought another mass of about 90 mg (the source mass) within a few millimeters of one of the masses onto the rod (the test mass), changing the position from time to time and thus the ultra-weak gravitational field of the source modulated. mass acting on the test mass. The modulated gravitational field caused the suspension rod to undergo small rotational oscillations. A Faraday shield (a gilded aluminum screen) was used to suppress electromagnetic interactions between the masses. The motion of the test mass was measured by the displacement of a laser beam reflected by a mirror on the rod, and the distance between the test mass and the source mass was measured with a camera (not shown). These measurements were used to measure the value of G, the fundamental constant used in calculations of gravitational effects.
A calculation using Newton’s law of gravity shows that the force acting between two spherical masses of 90 mg and a mass center of 2.5 millimeters (approximately the parameters of Westphal and colleagues’ experiment) is only about 9 × 10.–14 newton. This is about the same force acting on a mass of 9 picograms (1 pg is 10–12g) in the Earth’s gravitational field; to put it in perspective, 9 pg is about one third of the mass of a human red blood cell15. The big challenge, therefore, was to extract this extremely small gravitational signal from the background ‘noise’ in the experiment and from the effects of other forces (such as electromagnetic interactions) that become stronger than gravitational forces when the source and test mass are separated by small. distances.
Westphal et al. thus modulated the signal by periodically changing the position of the source mass with respect to the test mass in the torque balance. Due to the time-dependent gravitational interaction, the balance in the horizontal plane swung against the frequency of the signal modulation (12.7 millihertz). Because the gravitational field of a spherical mass is non-linear (a consequence of Newton’s inverted square law), the balance is also stimulated to oscillate at higher frequencies that are multiples of the modulation frequency (known as higher harmonics). This effect could be clearly identified in the experiment, thus providing a signature of the gravitational coupling between the masses.
The detection of such a minuscule gravity signal is itself an exciting result, but the authors went even further by a value for G from their experiment. Their estimate deviates from the internationally agreed value (see go.nature.com/2bwkrqz) by about 9% – a small amount, as the experimental uncertainties of their system have not yet been optimized for accurate measurements of G. The experiment is thus the first to show that Newton’s law of gravity even applies to such small source masses.
The next step is to move on to even smaller masses – Westphal et al. suggests that gravitational fields of masses of the order of 10–8kg could finally be measured. However, a lot of work will have to be done to achieve this goal. The first task is to significantly reduce the vibration of the vibration balance, which will not be easy. But if this can be done, the quantum gravitational effects may eventually be observed.